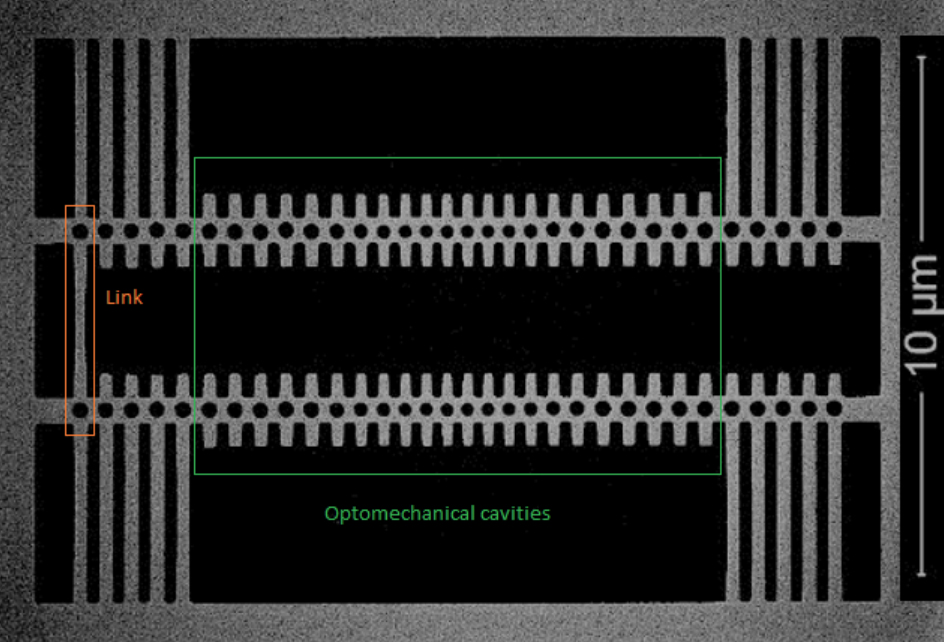
Synchronisation was discovered in 1665 by Lord Huygens reporting on his experiments on two pendulum clocks. So far synchronisation has been studied extensively at macroscopic scales. Not so in the nanoscale regime. And why not? Because it is challenging to obtain similar results in that regime: the design of the structures, the fabrication tolerances and the measurement methodology must be reproducible. Essential to spontaneous synchronisation between two systems are specific conditions: both systems must be self-sustained oscillators, meaning that they are able to generate their own rhythms, without the need of an external source. Moreover, they must synchronise due to a weak interaction, i.e., not because the systems are strongly connected. In our research these two conditions were unambiguously fulfilled for the first time, for two coupled nanobeams or optomechanical oscillators (see Fig. 1), which are 10 000 times smaller than Huygens’ pendulum clocks. The coupling was engineered as a narrow beam at one end of the oscillators. Unlike Huygens’ pendulums, which were driven by the mechanical motion of the clock, our OM oscillators are driven to self-sustained oscillations by means of radiation pressure forces exerted on them by infrared lasers. Each oscillator, A and B, receives light from a different laser, reaching its own vibration frequency. Oscillator A is set to have stronger oscillations, i.e., a larger amplitude than oscillator B. The experiment shows that thanks to the design of the beam linking them, the frequency of B becomes that of A, thus achieving synchronisation. We were able to control the collective dynamics (the synchronised state) and concluded that the more oscillators there are, the less noise the system generates, yielding better defined frequencies.
This research sets a firm basis towards reconfigurable networks of nano-optoelectro-mechanical oscillators for applications in, e.g., neuromorphic photonic computing, a field of research that intends to imitate neurological structures to improve computation.
Reference
Colombano MF, Arregui G, Capuj N E, Pitanti A, Maire J, Griol A, Garrido B, Martinez A, Sotomayor- Torres CM & Navarro-Urrios D 2019, ‘Synchronization of Optomechanical Nanobeams by Mechanical Interaction’, Physical Review Letters, 123, 017402.
Featured in Physics World Viewpoint https://physicsworld.com/a/independent-optomechanical-nanooscillators- vibrate-in-sync/ and in APS Synopsis https://physics.aps.org/synopsisfor/ 10.1103/PhysRevLett.123.017402
