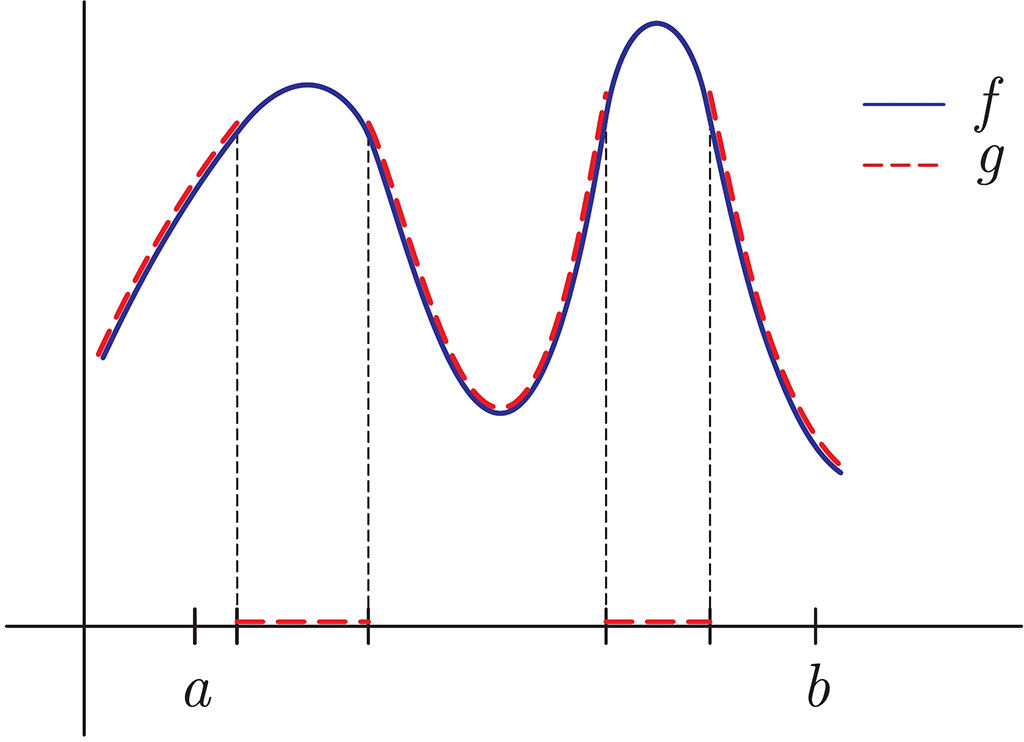
Take your favorite function f(x) on an interval [a,b]. Let us slightly modify it as follows. On a smaller interval (or a couple of intervals), redefine it to be zero. Is it possible that the maxima of the original function f(x) and the modified one g(x) are comparable in some sense? In general, the answer is NO since the original function might be huge exactly on the smaller interval. However, this is true for some special classes of functions, in particular, for polynomials. A proof of this fact as well as the precise meaning of comparability are obtained in this work.
More formally, we find a sharp constant C in the so-called Remez inequality max1 |f(x)| < C max2 |f(x)| in the case when f(x) is a trigonometric polynomial of a certain degree. Here the maximum max1 is taken over all x ∈ [a,b] and the maximum max2 is taken over all x ∈ [a,b]\B for a measurable set B. This problem was open for a long time even though a similar result for algebraic polynomials was obtained already in 1936.
Reference
Tikhonov S & Yuditskii P 2020, ‘Sharp Remez inequality‘, Constr. Approx. 52, no. 2, 233–246.
